
Figure 1 - Straight Stairs
The biggest obstacle to building a straight run set of stairs is space.
Besides requiring the "Total Run" of the stairs you need additional space at the bottom of the stairs in order to create a landing, which, at a minimum is the width of the stairs.
Stairs have some dimensional flexibility. However, there are guidelines and building codes which have set some minimum and maximum staircase design rules and numbers.
The one dimension that has no flexibility is the "Total Rise" as shown in Figure 2. This is the height of the staircase from the top of the finished basement floor to the top of the finished floor at the top of the stairs.
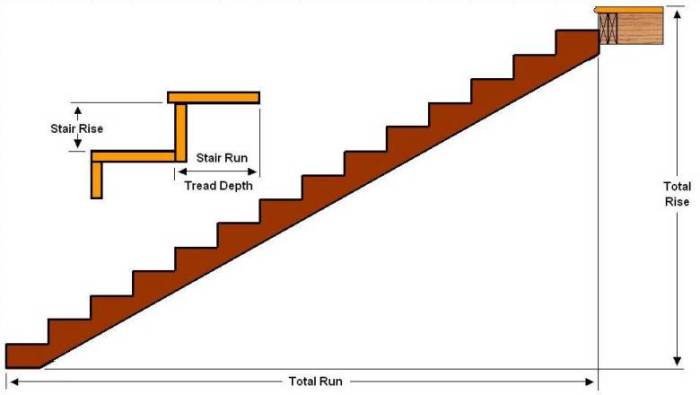
Figure 2 - Straight stairs showing total rise and total run
Table 1 - Fraction To Decimal Conversions |
|||||||
| Fraction | Decimal | Fraction | Decimal | Fraction | Decimal | Fraction | Decimal |
1/32 |
0.0313 |
9/32 |
0.2813 |
17/32 |
0.5313 |
25/32 |
0.7813 |
1/16 |
0.0625 |
5/16 |
0.3125 |
9/16 |
0.5625 |
13/16 |
0.8125 |
3/32 |
0.0938 |
11/32 |
0.3438 |
19/32 |
0.5938 |
27/32 |
0.8438 |
1/8 |
0.125 |
3/8 |
0.375 |
5/8 |
0.625 |
7/8 |
0.875 |
5/32 |
0.1563 |
13/32 |
0.4063 |
21/32 |
0.6563 |
29/32 |
0.9063 |
3/16 |
0.1875 |
7/16 |
0.4375 |
11/16 |
0.6875 |
15/16 |
0.9375 |
7/32 |
0.2188 |
15/32 |
0.4688 |
23/32 |
0.7188 |
31/32 |
0.9688 |
1/4 |
0.25 |
1/2 |
0.5 |
3/4 |
0.75 |
1 |
1 |

Note: You will have to round decimal places to the closest 1/32 of an inch on conversion from decimal to fraction, see Table 3.
To determine the width of each step and the height of each riser you start with the "Total Rise" measurement. From this dimension you can determine how many risers and the height of each riser or stair. Most building codes have set a maximum stair rise of 7 3/4". For the purpose of this example we will use a "Total Rise" of 106 3/4".
The calculation to determine how many risers you require is:
A Total Rise ÷ Max. Stair Rise = Number Of Risers
106 3/4 ÷ 7 3/4 = 13.77
As it is impossible to have a fraction of a number of risers, the number obtained is rounded off to the next highest whole number, in this case 14.
